惠斯通电桥

　　惠斯通电桥（英语：Wheatstone bridge，又称惠斯登电桥、惠斯同电桥）是一种测量工具，于1833年由塞缪尔·亨特·克里斯蒂发明，1843年由查尔斯·惠斯通改进及推广。它用来精确测量未知电阻器的电阻，原理与原始的电势差计相近。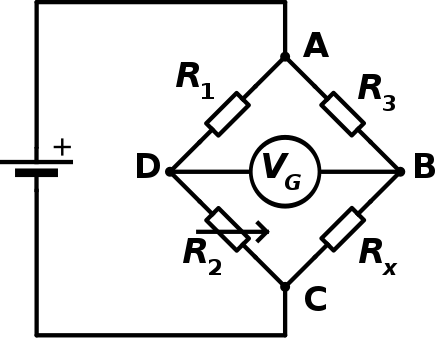

　　待测电阻{\displaystyle R_{x}}R_{x}，和已知电阻的可变电阻器{\displaystyle R_{2}}R_{2}、电阻{\displaystyle R_{1}}R_{1}和电阻{\displaystyle R_{3}}R_{3}。在一个电路内，将{\displaystyle R_{1}}R_{1}和{\displaystyle R_{2}}R_{2}串联，{\displaystyle R_{3}}R_{3}和{\displaystyle R_{x}}R_{x}串联，再将这两个串联的电路并联，在{\displaystyle R_{1}}R_{1}和{\displaystyle R_{2}}R_{2}之间的电线中点跟在{\displaystyle R_{3}}R_{3}和{\displaystyle R_{x}}R_{x}之间的电线中点接驳上一条电线，在这条电线上放置检流计。当{\displaystyle R_{2}/R_{1}=R_{x}/R_{3}}R_{2}/R_{1}=R_{x}/R_{3}时，电桥平衡，检流计无电流通过。由于是否有电流经过是十分敏感的，惠斯登桥可以获取颇精确的测量。

推导

　用基尔霍夫电路定律计算通过B和D的电流：

　　{\displaystyle I_{3}\-I_{x}\+I_{g}=0}I_{3}\-I_{x}\+I_{g}=0

　　{\displaystyle I_{1}\-I_{g}\-I_{2}=0}I_{1}\-I_{g}\-I_{2}=0

　用基尔霍夫第二定律计算ABD和BCD的电压：

　　{\displaystyle-(I_{3}\cdot R_{3})+(I_{g}\cdot R_{g})+(I_{1}\cdot R_{1})=0}{\displaystyle-(I_{3}\cdot R_{3})+(I_{g}\cdot R_{g})+(I_{1}\cdot R_{1})=0}

　　{\displaystyle-(I_{x}\cdot R_{x})+(I_{2}\cdot R_{2})-(I_{g}\cdot R_{g})=0}{\displaystyle-(I_{x}\cdot R_{x})+(I_{2}\cdot R_{2})-(I_{g}\cdot R_{g})=0}

　当电桥平衡时，{\displaystyle I_{g}=0}I_{g}=0。因此，以上的方程可以写成：

　　{\displaystyle I_{3}\cdot R_{3}=I_{1}\cdot R_{1}}I_{3}\cdot R_{3}=I_{1}\cdot R_{1}

　　{\displaystyle I_{x}\cdot R_{x}=I_{2}\cdot R_{2}}I_{x}\cdot R_{x}=I_{2}\cdot R_{2}

　两式相除，并整理，得：

　　{\displaystyle R_{x}={{R_{2}\cdot I_{2}\cdot I_{3}\cdot R_{3}}\over{R_{1}\cdot I_{1}\cdot I_{x}}}}R_{x}={{R_{2}\cdot I_{2}\cdot I_{3}\cdot R_{3}}\over{R_{1}\cdot I_{1}\cdot I_{x}}}

　由于串联电路内各元件的电流相等，故{\displaystyle I_{3}=I_{x}}I_{3}=I_{x}且{\displaystyle I_{1}=I_{2}}I_{1}=I_{2}。因此，{\displaystyle R_{x}}R_{x}的值为：

　　{\displaystyle R_{x}={{R_{3}\cdot R_{2}}\over{R_{1}}}}R_{x}={{R_{3}\cdot R_{2}}\over{R_{1}}}

　如果知道了四个电阻的值和电源的电压（{\displaystyle V_{s}}V_s），则可以算出每一个分压器的电压，并把它们相减，来得出电桥两端的电压（{\displaystyle Vg}{\displaystyle Vg}）。方程为：

　　{\displaystyle Vg={{R_{x}}\over{R_{3}+R_{x}}}V_{s}-{{R_{2}}\over{R_{1}+R_{2}}}V_{s}}{\displaystyle Vg={{R_{x}}\over{R_{3}+R_{x}}}V_{s}-{{R_{2}}\over{R_{1}+R_{2}}}V_{s}}

　可简化为：

　　{\displaystyle Vg=\left({{R_{x}}\over{R_{3}+R_{x}}}-{{R_{2}}\over{R_{1}+R_{2}}}\right)V_{s}}{\displaystyle Vg=\left({{R_{x}}\over{R_{3}+R_{x}}}-{{R_{2}}\over{R_{1}+R_{2}}}\right)V_{s}}

推广到交流电的情况

　　如果电桥两端接入的是交流电，如果使用交流电的复数表示法，即四个元件的阻抗分别为{\displaystyle Z_{1}}Z_{1}，{\displaystyle Z_{2}}Z_{2}，{\displaystyle Z_{3}}Z_{3}，{\displaystyle Z_{4}}Z_{4}，相位分别为{\displaystyle\phi _{1}}\phi _{1},{\displaystyle\phi _{2}}\phi _{2},{\displaystyle\phi _{3}}\phi _{3},{\displaystyle\phi _{4}}\phi _{4}，则在平衡状态有以下两个方程：

　　{\displaystyle{\boldsymbol{Z_{1}Z_{4}=Z_{2}Z_{3}}}}{\boldsymbol{Z_{1}Z_{4}=Z_{2}Z_{3}}}

　　{\displaystyle{\boldsymbol{\phi _{1}+\phi _{4}=\phi _{2}+\phi _{3}}}}{\boldsymbol{\phi _{1}+\phi _{4}=\phi _{2}+\phi _{3}}}

变化

• 　　电感：麦克斯韦桥

• 　　低电阻：凯文桥

关于惠斯通电桥，小编为大家就分享这些。欢迎联系我们合运电气有限公司，以获取更多相关知识。